KB.5 Operasi Vektor | Fisika X Sem. 1 KD 3.2

 

Assalamualaikum anak-anak sekalian berikut adalah materi lanjutan dari vektor yaitu Operasi Vektor.

setelah mempelajari materi ini diharapkan peserta didik dapat meneyelesaikan masalah operasi vektor dan menggambar vektor dengan beberapa metode tertentu. untuk materi selanjutnya silahkan pelajari materi berikut :

Selamat Membaca 😀

B.     Operasi Vektor

1.      Penjumlahan Vektor secara Geometris

Penjumlahan vektor secara geometris dapat dilakukan dengan dua macam metode yaitu metode poligon dan metode jajar genjang. Vektor hasil penjumlahan dinamakan vektor resultan

a.    Penjumlahan Vektor dengan metode Poligon

Pada metode ini, tahapannya sama dengan metode segitiga hanya saja metode ini untuk menjumlahkan lebih dari dua vektor. Vektor-vektor yang akan dijumlahkan secara poligon dapat dipindah-pindahkan asal panjang dan arahnya tidak diubah.

Langkah-langkah:

1. Gambarkan vektor A
2. Gambarkan vektor B dengan cara meletakkan pangkal vektor B pada ujung vektor A.
3. Gambarkan vektor C dengan cara meletakkan pangkal vektor C pada ujung vektor B.
4. Tariklah garis dari pangkal vektor A ke ujung vektor C
5. Vektor resultan merupakan vektor yang mempunyai pangkal di vektor A dan mempunyai ujung di vektor C.

Contoh:

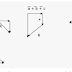
Jumlah ketiga buah vektor A, B, dan C dengan metode poligon.

 

                              A

                                                     B                         C           

Jawaban: Resultan ketiga vektor R = A + B + C

                                                                

                                               

                                                                       

                                        

b.  Penjumlahan Vektor dengan metode Jajar Genjanng

Cara menggambarkan vektor resultan dengan metode jajaran genjang, maka tahap-tahap adalah sebagai berikut:

Langkah-langkah:

1. Lukis vektor pertama dan vektor kedua dengan titik pangkal berimpit.
2. Lukis sebuah jajaran genjang dengan kedua vektor tersebut sebagai sisi-sisinya.
3. Resultannya adalah sebuah vektor yang merupakan diagonal dan jajaran genjang tersebut dengan titik pangkal sama dengan titik pangkal kedua vektor tersebut.

Gambarkan Vektor : R = A + B

Contoh:                                                          jawaban :                                                        

            A                     B                                

                                   

 

2.      Penjumlahan Vektor secara Analitis

 

 

 

 

 

Vektor R adalah vektor hasil penjumlahan(Vektor Resultan)  antara vektor A dan B dengan sudut antara vektor A dan B adalah . Besar vektor resultan R dari dua vektor A dan B yang membentuk sudut  dirumuskan sebagai berikut:

R = |R| =  √ A² + B² + 2 AB cos α

Penjumlahan vector secara analitis adalah menjumlahkan beberapa vector dengan cara menghitung semua komponen horizontal dan komponen vertical.

Contoh Soal :

1.      Dua buah perahu A dan B bergerak dengan kecepatan 5 m.s^–1 dan 7 m.s^–1 serta membentuk sudut 60⁰. Tentukan resultan kecepatan perahu.........

Diketahui :

                        A = 5 m/s

                        B = 7 m/s

                        α= 60

Ditanya  : |R| =....... ?

Jawab :

|R| = 

|R| = 

     |R| = 

     |R| = 

     |R| = 

 

Materi lengkap dan latihan soal selanjutnya silakan download materi pada link berikut :

DOWNLOAD MATERI OPERASI VEKTOR